Electrical activity of the heart is the essential issue for the cardiovascular physiological functioning. On this basis, Electrocardiogram (ECG) is one of the most relevant and representative measure of cardiac activity, mainly due to its clinical applications for monitoring and diagnosis. This work investigates the electrical activity of the heart exploring a mathematical model. Synthetic ECGs are generated representing a great variety of cardiac responses including normal and pathological behaviors. This strategy is useful to highlight distinct kinds of behavior, being interesting for clinical purposes. In this regard, a mathematical model is presented, being employed to develop numerical simulations that are compared with real ECGs. Deterministic and non-deterministic situations are treated showing the possibility of the combination of nonlinear and random aspects to define the rhythmic complexity. Different tools are employed in order to show interesting possibilities that can help the rhythm observations.

Cardiac rhythms; ECG; Nonlinear dynamics.

Natural systems exhibit a rich variety of behaviours that can be understood from a dynamical perspective. The complexity of responses is driven by physical and chemical phenomena that are intrinsically nonlinear [1]. Biological rhythms are considered one of natural manifestations of great interest for scientific research, especially dealing with health management and disease treatment. Rhythms can present regular or irregular behaviors that can be related to biological functioning, which can be healthy or pathological. On this basis, dynamics perspective is useful for biological system analysis and introduces the possibility to the use of proper tools that are able to provide more accurate classification that, ultimately, helps the clinical knowledge and diagnosis.

Heart rhythms receive a lot of attention due to their essential role in organism functioning. The Electrocardiogram (ECG) records cardiac electrical activity in the form of waves, which allow the identification of the electrical activity in different areas of heart, being useful to infer heartbeat rate. ECG has a widespread use due to its non-invasive characteristics. The electrical activity is recorded in the form of waves, and three important components should be pointed out: P wave, QRS complex and T wave. P wave represents the impulse generated by the SA node. The QRS complex is formed by ventricular contraction. T wave reflects ventricular repolarization when cardiac cells return to state in which they are ready to react to another stimulus. Although normal ECG is apparently periodic, it is usual to present Heart Rate Variability (HRV) that can be measured from R-R intervals. The Physionet repository [2] contains several relevant ECG databases as PTB (Physikalisch-Technische Bundesanstalt), MIT-BIH arrhythmia (Harvard-MIT Division of Health Sciences and Technology) and INCART (St. Petersburg Institute of Cardiological Technics). Reviews about ECG databases are found in Merone et al.[3] and Flores et al.[4].

Signal processing and monitoring analysis related to clinical applications is related to various research efforts. Due to unavoidable noise existence, proper techniques need to be employed [5]. R peak detection is treated by some references [6-9], and the calculation of heart rate variability and breathing are treated by [10] and [11]. Kaszala and Ellenbogen [12] reviewed sensors employed in cardiac devices according to different purposes: rate modulation, heart failure monitoring, sleep-disordered breathing and arryhmia discrimination. Defaye et al. [13] conduced the DREAM European study to evaluate the sleep apnea monitoring algorithm by implementing a transthoracic impedance sensor. Brisben et al. [14] introduced an algorithm to detect ventricular arrhythmia, which reduces T wave over-sensing without compromising tachycardia detection. Barold [15] presented a review of atrial arrhythmias detection algorithms of St. Jude Medical (Abbott). All these citations are related to real data, being useful to build databanks and develop theoretical and clinical knowledge.

An alternative way to analyze cardiac rhythms is by using mathematical models. The main advantage of this strategy is the reproduction of the most relevant characteristics of the involved phenomena, avoiding the necessity of dealing with large data banks. Van der Pol and Van der Mark [16] presented the pioneer work related to the mathematical modeling of heartbeats using nonlinear oscillators as motivation. Grudzinski and Zebrowski [17] proposed alterations of the original Van der Pol (VdP) oscillator into a more accurate description of the natural pacemaker. Dos Santos et al. [18] employed the coupling of two modified VdP oscillators representing Sinoatrial (SA) and Atrioventricular (AV) node functioning. Gois and Savi [19] developed a three-coupled oscillator model in order to represent ECG signals, where oscillators represent SA and AV nodes and His-Purkinje (HP) complex. This model is able to capture several behaviors including normal and pathological functioning. Cheffer et al. [20] improved the model due to Gois and Savi [19] by alterations on coupling terms. Besides, nonlinear dynamics tools are applied to assist rhythm identification and possible routes from normal functioning to pathologies. Cheffer and Savi [21] and Cheffer et al. [22] introduced statistical aspects showing that combination of nonlinearities and randomness can provide a greater variety of response, generating even more realistic ECGs.

Different approaches involving cardiac dynamical analysis by mathematical models can be cited as for instance: the modeling of tissues capable of represent flutter and fibrillation [23,24]; the investigation of mechanisms that initiate and support arrhythmias [25-28]; and the evaluation of the influence of external factors, such as breathing [29,30] and chemical regulators [31]. Historical reviews are additional references that need to be highlighted [32,33].

Mathematical models are also useful for control purposes. Garfinkel et al. [34,35] developed the first experiment of chaos control on biomechanical systems, applying the OGY method [36] on rabbit cardiac muscle. Ferreira et al. [37] designed controllers for natural pacemaker while Ferreira et al. [38] applied this idea for the cardiac system. Lounis et al. [39] employed high-order chaos control on cardiac model due to Quiroz-Juarez et al. [40]. Khan and Nigar [41] presented an active control technique that is a combination of synchronization and uncertainty concepts.

In this regard, clinical applications on device therapy can be cited as possible cardiac control approaches. Carlson et al. [42] presented results of study called Atrial Dynamic Overdrive Pacing Trial (ADOPT) to investigate the efficiency of the AF Suppression Algorithm (St. Jude Medical Cardiac Rhythm Management Division, Sylmar, California). Kamdar et al. [43] promoted a prospective comparison between QuickOpt algorithm [44] and echocardiography performances in optimization of atrioventricular and interventricular intervals for cardiac resynchronization therapy. For the same treatment purpose, Martin et al. [45] investigated an adaptive algorithm that allows two pacing techniques selection. Cadrin-Tourigny et al. [46] developed a novel model for individual prediction of arrhythmogenic right ventricular cardiomyopathy.

This paper deals with the analysis of the heart functioning, represented by its electrical activity, using a nonlinear dynamics perspective. A mathematical model is employed to represent the cardiac system behavior allowing the generation of synthetic ECG signals. Deterministic and non-deterministic situations are treated showing the importance of the combination of nonlinear and random effects to describe natural systems. A collection of results is discussed showing a great variety of cardiac behaviors, passing from normal to pathological rhythms [20,21]. The main goal is to mimic clinical characteristics highlighting the capabilities of the mathematical model to represent of different electrical activity of the cardiac system, using ECGs as reference. Nonlinear dynamics perspective is of concern employing tools as state space and Poincaré maps that show to be useful as alternative visualization of ECGs. Mathematical models can be exploited in algorithms for device therapy and rhythm identification purposes.

After this introduction, the paper is organized as follows. Cardiac system mathematical model is presented. Results of numerical simulations are shown for relevant heart rhythm behaviors highlighting physiological aspects and their effects on ECGs. Finally, conclusions are discussed.

Cardiac system functioningis modeled based on the electrical activity of the heart and represented by ECG. Mathematical model is built considering three fundamental nodes: Sinoatrial node (SA), Atrioventricular node (AV) and His-Purkinje complex (HP). Each one of these nodes is described by a nonlinear oscillator represented by the model due to Grudzinski & Zebrowski [17], described by the following equation,

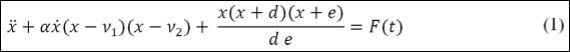
where x represents the electrical activity and the dot represents time derivative; α defines the pulse shape, characterizing the time when the heart receives the stimulus; ν₁ and ν₂ determine the signal amplitude, and to preserve the self-excitatory nature, ν₁ν₂< 0; and F(t) is an exter- nal stimulus.

The coupling of these oscillators is performed by asymmetrical and bidirectional connections [19,20]. Figure 1 shows the concep- tual model of this approach where it is important to highlight that the general model presents situations that do not occur in the normal functioning, but they are considered in order to describe all possible conditions including pathologies. Besides, external stimulus is incor- porated allowing the possibility to consider external factors as device treatments, physical exercises or abnormal electrical conditions. Cen- tral nervous system stimuli are represented by self-excitatory behavior which means that external stimulus are from situations different of the normal functioning.

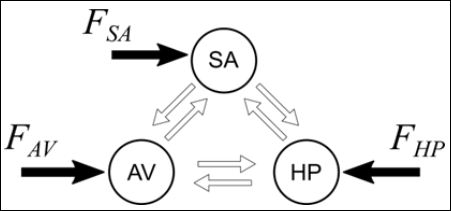
Figure 1: Conceptual model of the general cardiac functioning represented by Si- noatrial node (SA), Atrioventricular node (AV) and His-Purkinje complex (HP) with asymmetrical and bidirectional connections.FSA, FAV and FHP are external stimuli.

Under these assumptions, by considering that x=[x1 x3 x5 x2 x4 x6]T is the state variable vector, where xi, xi+1 (i=1,3,5) represents the vari- able and its time derivative of each one of the oscillators represented by equation (1). Based on that, the system dynamics is governed by the following equations [21].

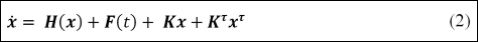
Where x^τ is the delayed state vector, given by,

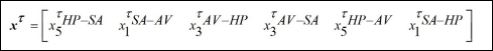
System dynamics is represented by the following equations,

The vector of external stimuli is presented in the sequence, representing a reduced order description of spatiotemporal aspects,

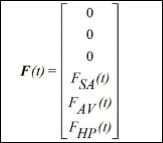
The coupling terms are represented by the following matrix,

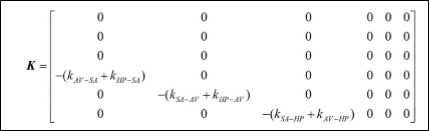
while the delayed couplings are represented by the matrix,

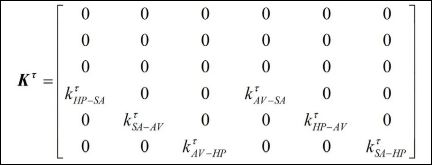
It should be pointed out that, by considering that indexes m and n represent SA, AV or HP, being m ≠ n, k_m-n and k^τ are coupling coefficients between m and nnodes

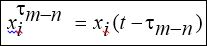
are delayed terms  where t[s]: t = [bt ] = st is the time delay; and Fm = rm sin(wmt) is an external excitation that represents spatiotemporal stimulus.

The ECG is represented by a combination of the signal of each one of the oscillators, being formed by a linear combination of the state variables given by [19]. 

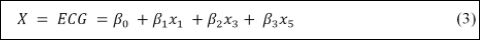
where β0, β1, β2 and β3 are constants. Therefore,

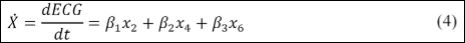
Since governing equations are presented in dimensionless form, it is interesting to define a dimensional time t[s]: t = βtt  where [bt ] = s can be estimated by the ratio between real RR interval,RRreal, and numerical RR interval, RRnum :βt  =  mean (RRreal ) / mean(RRnum 

The model parameters are adjusted based on the same real ECG data and can be either deterministic or non-deterministic. Determin- istic situations consider that each rhythm is associated with a set of parameters and, a change of this behavior is due to some parameter change. In other words, pathological rhythm can be understood as an evolution from the parameter change. On the other hand, non-de- terministic situations present parameter random variation which can induce pathological rhythms.

Randomness is treated assuming that coupling parameters are modeled as normal distributions around a nominal value represented by the mean with standard deviations. Therefore, coupling terms can be written as follows

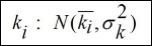
where ki is the mean, nominal value, and  is the standard deviation of the normal distribution.

Numerical procedure to integrate governing equations is related to a classical Runge-Kutta method together with some interpolation to define delayed states. For more details, see Cheffer et al. [20,21].

A typical ECG is the time history of the signal measured by sensors in specific positions. An alternative visualization can be defined by considering state space or phase plot that considers a plot of a variable and its time derivative. Specifically, it is possible to define the vector {X, Ẋ}. Poincaré map can also be employed to highlight the dynam- ical aspects of the ECG defining a stroboscopic representation of the dynamical system response. There are different ways to build a Poin- caré map and, among them, it should be pointed out the reference period strategy. This procedure consists of arranging various planes spaced by a period T through time, as presented in the schematic pic- ture of figure 2. Poincaré map is the set of intersecting points between the system response (red) and planes (blue), which allows a dimension reduction turning the continuous time into a discrete set of states.

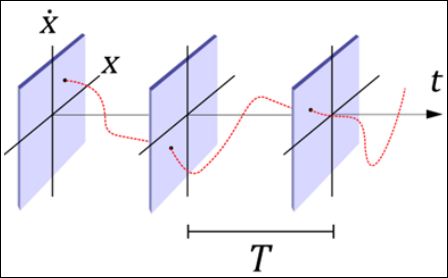
Figure 2: Schematic picture of Poincaré map built using a reference period that defines the stroboscopic sample time.

This section presents results of numerical simulations establishing comparisons with real ecgs from physionet databases. Different cardiac rhythms are of concern in order to show normal and pathological behaviors. A brief description of each rhythmis presented trying to highlight the main characteristics that mathematical model can reproduce.

Figure 3 shows ECGs for six cardiac rhythms: normal, atrial flutter, atrial fibrillation, ventricular flutter and two types of ventricular fibril- lation. Each panel of the figure is associated with a specific rhythm represented by the following pictures: real ECG (black), synthetic ECG (red), state space of synthetic ECG (red) and poincaré maps of synthetic ECG (blue). Appendix 1 presents system parameter em- ployed for each one of the responses.

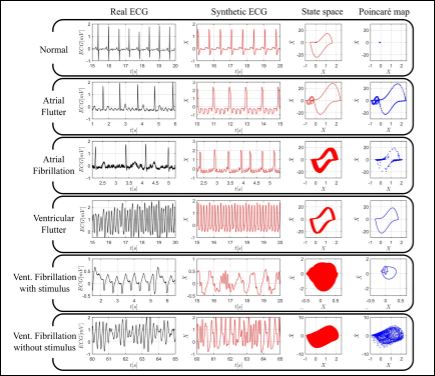
Figure 3: Numerical simulations related to deterministic approach. Real (black – column 1) and synthetic (red – column 2) ECGs, state spaces (red – column 3) and Poincaré maps (blue – column 4) for different rhythms: normal, atrial flutter, atrial fibrillation, ventricular fibrillation, ventricular fibrillation with stimulus and ventricular fibrillation without stimulus.

Normal rhythm is shown in first panel of the figure and it is possi- ble to verify that the main characteristics represented by P, QRS and T waves, are qualitatively well reproduced. State space is a closed curve with two loops: A smaller around {0,0}, referring to P and T waves; and a larger, associated to QRS complex. Poincare map is represented by a single point. The normal rhythm is the reference case, being con- sidered as a cardiac signature in such a way that all other rhythms are understood as deviations of this signature.

Atrial flutter with 4:1 conduction is presented in the second panel. The characteristic p-waves with “sawtooth” form, called f waves [47], are well defined. State space is a closed curve, but with an increased larger loop and smaller loops increased and left-shifted. Poincaré map is a set of points associated with a closed curve.

Atrial fibrillation is presented in the third panel, characterized by high frequency of small waves and irregular R-R intervals. State space is a thick region around larger loop. This region is composed by several trajectories, being associated with a closed curve and without clear presenting smaller loops. Poincaré map is a set of sparse points.

Ventricular flutter responses are displayed in the fourth panel be- ing characterized by sequential QRS complexes. Note that it is im- possible to identify p and t waves. State space is a thick region around larger loop, but more defined than previous case. Poincaré map is a closed curve with larger loop shape.

There are several types of ventricular fibrillation and two cases are of concern: With and without external stimuli. Both cases exhibit irregular, chaotic-like behaviors. ECG irregular behavior reflects in state spaces with filled regions, which represent the uncountable tra- jectories of these kinds of response. The fifth panel presents ventricu- lar fibrillation induced by a periodic stimulus applied to HP oscillator. This kind of fibrillation shows small amplitude oscillations, reflecting in a small, filled region in state space. Its poincaré map is an irregular closed curve. A ventricular fibrillation without external stimulus is presented in the sixth panel. It is observed an irregular response that is driven by only oscillator behaviors. This fibrillation presents oscilla- tions for both small and large amplitudes, which generates space state with greater filled region. Poincaré map is composed by an irregular cloud of points, called strange or chaotic-like attractor.

Probabilistic approach is now of concern by introducing random couplings between oscillators. Based on deterministic normal set of parameters, assumed to be constant, each coupling constant is consid- ered a stochastic variable that can vary in time based on a standard deviation. Basically, the procedure evaluates the effect of different levels of randomness over normal rhythm and indicates possible pa- thologies. More details can be found in Cheffer and Savi [22].

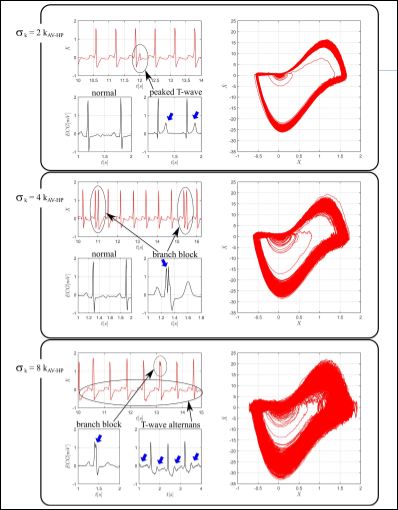
Figure 4: Numerical simulations related to non-deterministic approach. Real ECGs (black-column 1) and ECGs (red-column 2) and state spaces (red-column 3) of synthetic respons- es for different random AV-HP couplings: sk = 2k AV -HP , sk = 4k AV -HP and sk = 8k AV -HP .

Figure 4 presents results for three values of standard deviation of av-hp coupling. In each group, the values of are presented as multi- ples of nominal coupling constant presenting the following pictures: real ECGs (black), synthetic ECGs (red) and synthetic state spaces (red). The first panel presents responses with peaked T waves, high- lighted by blue arrows in real data and a circle in synthetic picture. Note that state space presents a region slightly denser than normal rhythm. The smaller loop scattering is associated with T waves and the increased thickness of larger loop is due to QRS deviations, imper- ceptible in ECG. The second panel presents results with incomplete branch block responses, characterized by double R peaks, highlighted in real and synthetic ECGs. The even thicker larger loop reflects the double R peaks. The third panel shows ECGs with highlighted T wave alternans, a clinical marker commonly used to predict sudden cardi- ac death [48], being associated with a more enlarged region around smaller loop in state space.

The analysis of cardiac rhythm from mathematical models is treat- ed. Nonlinear dynamics perspective indicate that state space visual- ization can capture fluctuations that are imperceptible in ECGs. In addition, Poincaré map shows to be a satisfactory tool to characterize dynamical characteristics. Based on that, both methods exhibit po- tential to be implemented in real-time ECG monitoring devices or ar- rhythmia discrimination algorithms. Due to the great range of behav- iors that the model can reproduce, it can also be used in algorithms for device therapy and rhythm identification purposes. In this regard, it should be highlighted that dynamical perspective is able to highlight pathological rhythms, which can be useful for rhythm identification.

The authors would like to acknowledge the support of the Brazilian Research Agencies CNPq, CAPES and FAPERJ.

Conflict of Interest